







6. TRASPOSIZIONE DEL MODELLO AI BACINI DI INTERESSE
Nel caso dei modelli black-box il problema della trasposizione può essere risolto applicando i parametri che definiscono i modelli di ciascun bacino osservato ai bacini parziali non osservati sulla base di opportuni criteri di similitudine idrologica. Tale operazione applicata al caso in esame comporta il trasferimento dei parametri gk, wk e dk. È evidente che la trasposizione del parametro gk implica anche la trasposizione delle medie mensili e in particolare la media dei deflussi. Verifiche preliminari hanno però messo in evidenza che per le sezioni più montane il deflusso medio è notevolmente superiore a quello che risulta dall’applicazione del criterio indicato. Tale circostanza ha condotto a riformulare su basi diverse il criterio di trasposizione ipotizzando che la sua validità si limitata ai soli parametri wk e dk e che i parametri gk vadano invece rideterminati, per ciascun bacino d’interesse, sulla base di una valutazione del tutto indipendente.
Il problema legato alla stima delle medie dei deflussi mensili è suscettibile di una prima semplificazione dall’osservazione empirica che l’andamento del deflusso medio annuo non presenta differenze molto accentuate da bacino a bacino. Ciò autorizza a ritenere che tali differenze siano praticamente trascurabili nell'ambito dei bacini di interesse contenuti entro lo stesso bacino parziale osservato. Ne consegue che, una volta noto il deflusso medio annuo per ciascun bacino di interesse, la relativa ripartizione mensile può essere ottenuta per semplice proporzionalità da quella del pertinente bacino osservato. In definitiva il problema della trasposizione dei modelli della funzione di trasferimento si riconduce a quello del deflusso medio annuo di ciascun bacino parziale non osservato.
6.1 Metodo adottato
Il problema della determinazione del deflusso medio annuo può essere ricondotto alla determinazione della superficie di deflusso relativa al territorio considerato. Tale superficie deve variare con continuità e deve per definizione essere sempre positiva.
Dopo attenta analisi si è stabilito procedere alla stima dell’altezza di deflusso puntuale in corrispondenza dei nodi della RPR. Questa impostazione presenta il grande vantaggio che, una volta ottenute tali stime, la forma della superficie di deflusso può essere completamente definita utilizzando gli stessi criteri già elaborati nella determinazione dell’afflusso ragguagliato. Più precisamente, poiché operando in tal modo resta individuata una rete di riferimento dell’altezza puntuale di deflusso del tutto coincidente con quella pluviometrica, i pesi relativi al calcolo dei corrispondenti valori ragguagliati risultano ovviamente gli stessi già adottati per l’afflusso sicché, detto Di il deflusso medio annuo relativo all’i-esimo pluviometro e detto ai il peso di tale apparecchio rispetto al j-esimo bacino osservato, il pertinente deflusso ragguagliato Dj si ricava dall’espressione:
![]()
essendo n il numero di pluviometri che influiscono sul bacino considerato.
In questa prospettiva, si consideri ora il caso ideale in cui si disponga dei deflussi medi annui Dj relativi a un numero di bacini pari al numero complessivo N degli apparecchi pluviometrici. In tale ipotesi segue immediatamente che la stima dei deflussi puntuali Di si ottiene risolvendo un sistema di N equazioni lineari. In realtà, in Sardegna, il numero dei bacini osservati è assai inferiore rispetto a quello delle stazioni pluviometriche sicché la soluzione del sistema è indeterminata a meno che non si impongano vincoli ulteriori. A questo punto si può ricorrere all’informazione pluviometrica introducendo opportune ipotesi sulla relazione che intercorre fra afflusso e deflusso puntuale. Sulla base di analisi svolte in merito alla relativa uniformità delle perdite entro ciascun sistema idrografico principale, si è ritenuto ragionevole assumere che la perdita apparente media annua sia praticamente costante per tutti i pluviometri associati ad uno stesso bacino parziale osservato. Il che equivale ad ipotizzare che la relazione fra afflussi e deflussi medi annui puntuali sia rappresentata localmente da una retta di coefficiente angolare unitario.
Poiché nel caso in esame i bacini parziali osservati sono in numero di 27 ed altrettante sono quindi le equazioni componenti il sistema, è allora necessario stabilire 27 gruppi di pluviometri che si ritiene caratterizzati dalla stessa perdita apparente. Detta infatti Pj la perdita puntuale relativa al gruppo di pluviometri associato al j-esimo bacino si avrà:
Di = -Pj + Ai
e quindi:
![]()
Tali relazioni formano il sistema di 27 equazioni lineari nelle 27 incognite Pj che una volta risolto consente di valutare il deflusso medio puntuale Di a ciascun pluviometro.
Per quanto riguarda la determinazione degli aggruppamenti dei pluviometri, il criterio che è apparso più naturale adottare è quello di basarsi sul peso che ciascun apparecchio ha rispetto a un determinato bacino osservato mantenendo comunque una certa elasticità nelle scelte.
Definiti in tal modo gli elementi principali del metodo, si deve osservare che questo non consente di evitare la possibile comparsa di valori negativi di deflussi medio annuo. Onde superare anche questo inconveniente si è deciso di modificare la relazione puramente lineare tra afflussi e deflussi sostituendo, nel campo degli afflussi minori, la retta D = -Pj + A con una tratto parabolico garantendo al contempo sia la continuità con il ramo lineare sia la positività dei deflussi.
In tal modo si perviene a un sistema di equazioni non lineari che richiede una procedura di soluzione numerica di tipo iterativo.
Per ciascun bacino parziale di interesse sono stati determinati quindi i deflussi medi annui attraverso l’operazione di ragguaglio e quindi i deflussi medi mensili ripartendo i valori annui proporzionalmente ai valori annui dei bacini osservati associati. Si è quindi applicato il criterio di trasferimento del modello nel senso che si sono assunti gli stessi valori dei parametri wk e dk corrispondenti ai bacini osservati e su questi si è applicato il modello black-box. In realtà il parametro wk è stato ulteriormente affinato, la funzione obiettivo essendo lo scarto tra le medie mensili dei deflussi calcolati e quelli ottenuti dalla procedura di ragguaglio. I parametri gk sono stati determinati mediante un semplice procedimento iterativo analogo a quello già utilizzato in sede di stima del modello.
6.2 Trasposizione del modello del rumore
Il modello della componente casuale del deflusso superficiale risulta caratterizzato all’interno di ciascun bacino parziale osservato da un’unica serie del residuo at alla quale corrisponde in base alla relazione R*t = F R*t-1 + at un’unica serie del rumore standardizzato. La serie del rumore relativa ai bacini d’interesse componenti (o contigui) sono stati messi in relazione a detto valore tramite dei coefficienti di proporzionalità. Detti bj tali coefficienti, j essendo l’indice del bacino di interesse, questi sono stati espressi tramite la relazione:
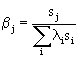
ove la sommatoria è estesa a tutti i bacini d’interesse, li è il rapporto fra la superficie parziale e quella complessiva mentre il termine sj è espresso dalla relazione:
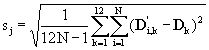
I coefficienti bj, pertanto, hanno la funzione di ripartire il rumore ai bacini osservati in proporzione al rapporto fra il deflusso medio annuo di ciascuno dei bacini componenti e quello complessivo.