







5. MODELLO DI TRASFERIMENTO AI BACINI OSSERVATI
Uno degli obiettivi dello studio è la ricostruzione delle serie storiche dei deflussi mensili alle sezioni di interesse in condizioni naturali, prescindendo cioè dalle utilizzazioni, con lo scopo di conseguire una valutazione dell’entità delle risorse potenzialmente disponibili e di ottenere informazioni sul relativo regime idrologico. L’impostazione scelta contempla la formulazione di un modello interpretativo del processo di formazione dei deflussi ai bacini osservati parziali, la stima dei relativi parametri con riferimento alle sezioni osservate e la successiva trasposizione ai bacini di interesse.
Di norma per deflusso ricostruito si intende esclusivamente la parte deterministica dei deflussi stessi che deriva dall’applicazione dei modelli senza porre in alcun conto la relativa componente stocastica di rumore. Ora, a ben vedere, le serie dei deflussi così ottenute non presentano di per sé alcuna utilità pratica a meno che la componente stocastica non sia trascurabile, il che è raramente il caso in campo idrologico. Non si può procedere allora ad uno studio di utilizzazione sulla base delle serie dei soli deflussi deterministici senza incorrere in errori di valutazione principalmente a causa della netta riduzione di varianza che presentano tali serie rispetto a quella delle serie naturali. Ai fini pratici quindi le serie storiche dei deflussi deterministici devono essere integrate con le corrispondenti componenti stocastiche costituite dalle serie storiche del rumore. Queste ultime, relativamente ai bacini non osservati, sono ovviamente incognite, ma possono essere stimate partendo da quelle note dei bacini osservati.
Prima di descrivere il modello idrologico adottato è opportuno procedere brevemente alla descrizione delle operazioni di ragguaglio che hanno consentito di confrontare grandezze non omogenee quali le altezze di pioggia misurate dai pluviometri e i deflussi naturali ai bacini studiati.
5.1 Afflussi ragguagliati ai bacini studiati
L’operazione di ragguaglio consiste nel trasferimento delle informazioni pluviometriche puntuali su tutta la superficie di un bacino. Il metodo adottato si basa sulla rete pluviometrica di riferimento che è organizzata secondo un network triangolare che soddisfa la condizione di continuità della superficie che rappresenta la grandezza considerata.
Il metodo presenta il vantaggio di condurre a una stima degli afflussi attraverso un set di pesi la cui determinazione è piuttosto semplice e che dipendono esclusivamente dalle caratteristiche geometriche del bacino in esame e dalle coordinate dei pluviometri interessati.
Infatti, considerata la porzione della superficie di un bacino contenuta all’interno di una maglia triangolare di indice m e i cui vertici siano tre pluviometri, di coordinate (xm,i, ym,i) appartenenti alla RPR, allora, dette xm, ym le coordinate del baricentro di tale porzione, il peso am,i del pluviometro i-esimo è dato dalla relazione:
am,i =1/(2 Sm) [( xm,i ym,k - xm,k ym,j) + (ym,j - ym,k) xm + (xm,k - xm,j) ym]
dove i 3 pesi am,i sono ottenibili per permutazione ciclica degli indici e Sm rappresenta la misura della superficie della maglia triangolare m-esima.
Il peso del pluviometro i sull’intero bacino sarà allora:
![]()
Ove S è l’area del bacino, n è il numero di triangoli che lo interessano e ovviamente la somma degli ai è uguale a uno.
Al fine di poter operare l’operazione di ragguaglio degli afflussi su tutti i bacini imbriferi (osservati e di interesse) presi in considerazione da questo studio si è operata la digitalizzazione dei confini di questi in formato vettoriale previa individuazione degli spartiacque. Il lavoro è stato effettuato sulla base della cartografia IGM in scala 1 : 100.000 con un grado stimato di indeterminazione inferiore ai 100 metri. Tali informazioni sono gestite direttamente dal programma che determina i pesi ai per tutti i bacini in esame. Dalle operazioni di ragguaglio si ottengono gli afflussi ai bacini osservati e di interesse che costituiscono uno degli input per le procedure di modellazione.
5.2 Modello adottato
In campo idrologico, com’è noto, esiste una notevole produzione di modelli atti ad interpretare il processo del deflusso superficiale. Fra questi è opportuno distinguere, anzitutto, quelli che si basano sulle sole osservazioni di deflusso da quelli che utilizzano anche altre informazioni di interesse idrologico e, segnatamente, quelle relative all’afflusso meteorico.
Appare evidente che, in presenza di una quantità notevole di osservazioni di deflusso, sia in termini spaziali che temporali, tale da consentire un’adeguata modellazione del fenomeno, può risultare del tutto superfluo il ricorso ad altre grandezze se l’interesse dello studio è rivolto esclusivamente al deflusso superficiale. Ma è altrettanto evidente che, nella maggior parte dei casi, la quantità delle osservazioni di deflusso è del tutto inadeguata ed appare pertanto spontaneo cercare di sfruttare al meglio le informazioni disponibili ricorrendo ad una modellazione del bacino imbrifero che regola la trasformazione della precipitazione meteorica in deflusso. Questo secondo tipo di modelli, comunemente noti come modelli di trasferimento o di "input-output" conducono ad una rappresentazione matematica del fenomeno tramite funzioni che a seconda delle scelte adottate potranno tenere conto dei fenomeni fisici coinvolti ovvero qualora il modello prescelto sia di tipo "black-box" prescinderanno assolutamente da tali variabili fisiche. I modelli concettuali costituiscono una categoria intermedia fra queste due essendo in qualche modo assimilabili a dei modelli fisici, ma caratterizzati da un formalismo estremamente semplificato e da un numero relativamente esiguo di parametri.
Per quanto concerne la Sardegna, non foss’altro che per la scarsità delle osservazioni di portata disponibili, si è portati senza ombra di dubbio a preferire un approccio legato all’utilizzo dei modelli di trasferimento.
Un secondo elemento distintivo dei modelli idrologici riguarda il passo temporale su cui operano. Si passa, infatti, da modelli a base oraria a modelli a base annuale in relazione alle finalità cui sono destinati. Ora, non c'è dubbio che i modelli a base oraria hanno il grande vantaggio di prestarsi a qualunque tipo di applicazione, compreso il controllo degli eventi di piena, ma, di contro, presentano il grave inconveniente di richiedere una mole di informazioni decisamente elevata che, oltre tutto, è quasi sempre indisponibile su scala regionale. Per queste ragioni sono stati ampiamente sviluppati anche modelli a base temporale più estesa e, in modo particolare, quelli a base mensile che sono considerati del tutto adeguati alle esigenze del settore applicativo che riguarda le utilizzazioni. A causa della periodicità annuale del processo di trasformazione afflussi-deflussi, non è però generalmente possibile formulare un modello unico per tutti i mesi dell’anno ma è di norma necessario tenere conto di tale periodicità introducendo una parametrizzazione stagionale o meglio ancora mensile del modello.
In definitiva si è scelto di applicare ai bacini osservati parziali una particolare classe di modelli di trasferimento comunemente nota come modello stocastico lineare o modello Box e Jenkins [5].
Il modello adottato è caratterizzato dai seguenti punti:
- differenziazione dei parametri in funzione del mese;
- presenza del solo afflusso come variabile di ingresso;
- presenza di un termine autoregressivo.
Avendo scelto di indicare con apici le variabili modellate e quindi senza apice quelle osservate, il modello adottato si può rappresentare mediante le due relazioni:
Di,k @ gk + wk Ai,k + dkD'i,k-1 + Ri,k se gk + wk Ai,k ³ 0
Di,k @ dkD'i,k-1 + Ri,k se gk + wk Ai,k < 0
avendo posto:
i indice di anno;
k indice di mese;
Di,k deflusso osservato del mese k;
wk, dk
parametri del modello (0£ wk£
1, 0£ dk£
1);
Ai,k afflusso mensile ragguagliato;
D'i,k-1 deflusso ricostruito del mese k-1;
Ri,k componente casuale (residuo).
Per quanto riguarda gk , la sua espressione è data da:
gk = Dk
- wk Ak
+ dk D'k-1
ove:
Dk media campionaria dei deflussi osservati
del mese k;
Ai,k valore medio degli afflussi del mese k;
D'k-1 valore medio dei deflussi ricostruiti
del mese k.
In fase di modellazione il parametro gk è calcolato con procedimento iterativo sulla base del vincolo che sia sempre soddisfatta la relazione Dk @ D'k-1 relativamente al periodo osservato.
Si noti che è stato introdotto un effetto soglia, tipicamente non lineare, tale che se l’afflusso meteorico non supera il valore A*k = - gk/wk esso non contribuisce affatto alla formazione del deflusso. Ai fini applicativi, è importante osservare che, considerando come ingresso la serie A'i,k , trasformata della Ai,k secondo le relazioni:
A'i,k = Ai,k se Ai,k ³ A*k
A'i,k = A*k se Ai,k < A*k
il modello si può compendiare nell’unica espressione:
Di,k = gk + wk A'i,k + dkD'i,k-1 + Ri,k
gk = Dk - wk A'k - dkD'k-1
Si badi che l’introduzione della suddetta soglia non è un semplice espediente atto a evitare che i deflussi calcolati possano assumere valori negativi. Questa scelta, infatti, corrisponde ad assegnare un ruolo ben definito alla componente autoregressiva che rappresenta quindi l’entità del deflusso mensile in assenza di afflusso eccedente, il che è, almeno in parte, conforme alla natura del fenomeno fisico.
Un’altra particolarità del modello consiste nel fatto che è stata introdotta una procedura atta a eliminare gli effetti dovuti alle piene eccezionali del mese di ottobre. Questa si fonda sul criterio di trattare diversamente la parte di afflusso eccedente un valore di soglia prefissato, A**10, che, dopo diversi tentativi, si è stabilito di determinare in base alla condizione standard:
(A**10 - m{A10})/s{A10} = 3.5
ove m{A10} e s{A10} sono, rispettivamente, la media e lo scarto dell’afflusso di ottobre. Ogni qual volta risulti Ai,10 > A**10, la quota A**10 viene utilizzata normalmente nel modello mentre la quota eccedente Ai,10 - A**10 si considera che contribuisca per intero a incrementare il valore di deflusso così ottenuto attribuendole, in sostanza, un coefficiente di deflusso unitario. Di tale incremento, peraltro, non si tiene alcun conto ai fini dell’applicazione del modello al mese successivo riducendo così l’effetto di persistenza che altrimenti si osserverebbe. La variante è stata introdotta esclusivamente per il mese di ottobre in ragione del fatto che solo per esso, come i controlli effettuati hanno indicato, le piene osservate sono a un livello così elevato rispetto alla norma da intervenire negativamente sulle prestazioni del modello base. Ciò è da imputare quasi esclusivamente all’assoluta eccezionalità dell’evento meteorico dell’ottobre 1951 che ha investito tutta l’isola esprimendosi con particolare virulenza soprattutto sul bacino del Flumendosa e su quelli finitimi. Naturalmente, questa particolarità del modello è stata adottata per tutti i bacini considerati nel presente studio anche se gli elementi necessari per la sua definizione sono stati tratti in realtà dalle osservazioni di quelle poche sezioni ove si sono verificati solo alcuni eventi con un effettivo carattere di eccezionalità.
Il modello descritto presenta il limite di non poter
tenere conto dei fenomeni di persistenza
[6] tipici di alcune variabili meteorologiche e climatologiche. Tali fenomeni,
ampiamente discussi in letteratura, sono di difficile previsione e modellazione
e vengono di norma studiati ricorrendo a tecniche di analisi spettrale
[7, 8] quale l’analisi di Fourier o le wavelets.
Il ciclo giornaliero e
stagionale hanno un evidente effetto sulle variabili climatologiche, che a loro volta
influenzano in modo ovvio il regime delle piogge.
Invece, i fenomeni di persistenza sono caratterizzati da frequenze atipiche, come le
oscillazioni quasi biennali, con periodo di 26 mesi; la notissima fluttuazione
comunemente nota come El Niño o ancora le oscillazioni
di periodo pari a undici anni che trovano una spiegazione nel
ciclo di attività delle macchie solari.
Si è, pertanto, ritenuto di dotare il modello della possibilità
di tenere conto di tali effetti introducendo una "baseline"
modellata con una funzione polinomiale. Vari tentativi hanno indotto ad adottare un polinomio di terzo
grado modellato sui totali annui degli afflussi espressi per anno idrologico.
La funzione polinomiale, il cui effetto sul modello è comunque assai
contenuto, viene introdotta come termine moltiplicativo rispetto alla variabile
A'i,k che viene quindi riscritta come:
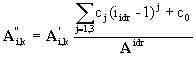
ove:
iidr è l'indice dell'anno idrologico corrispondente
agli indici i e k (iidr=1, ..., 71);
cj sono i coefficienti del polinomio;
Aidr è l'afflusso medio annuo (anno idrologico).
Un ultimo cenno merita la procedura di stima dei parametri. I bacini parziali (il cui elenco è riportato nella tabella seguente) sono stati divisi in due gruppi: il primo comprendente i bacini aventi un’unica sezione di misura e coincidenti in pratica con il proprio bacino totale, il secondo comprendente quei bacini contraddistinti da più di una sezione di misura e formanti quattro distinti "cluster" di bacini osservati (indicati in tabella come A, B, C e D).
| COD. |
Cluster |
Stazione | |
| 1 | 2 | MANNU DI S. SPERATE A MONASTIR | |
| 2 | 3 | CIXERRI A UTA | |
| 3 | 4 | RIO DI PALMAS A MONTI PRANU | |
| 4 | 6 | FLUMINIMAGGIORE A FLUMINIMAGGIORE | |
| 5 | 7 |
A |
TIRSO A RIFORNITORE TIRSO |
| 6 | 8 |
A |
TALORO ALLA PASSERELLA GAVOI |
| 7 | 9 |
A |
TIRSO A S. CHIARA D'ULA |
| 8 | 10 |
B |
ARAXISI A ORTO SCIAVICO |
| 9 | 11 |
B |
FLUMINEDDU O MASSARI AD ALLAI |
| 10 | 12 | TEMO A REINAMARE | |
| 11 | 13 | MANNU DI PORTO TORRES A PEDRAS ALVAS | |
| 12 | 14 |
C |
MANNU DI OZIERI A P.TE DELLA LEGNA |
| 13 | 15 |
C |
RIO DI BUTTULE A BUTTULE |
| 14 | 16 |
C |
MANNU DI OZIERI A FRAIGAS |
| 15 | 17 |
C |
MANNU DI BERCHIDDA A BERCHIDDA |
| 16 | 18 |
C |
RIO DI OSCHIRI A CONCARABELLA |
| 17 | 19 |
C |
COGHINAS A MUZZONE |
| 18 | 20 | LISCIA A LISCIA | |
| 19 | 21 | CEDRINO A CEDRINO | |
| 20 | 22 | FODDEDDU A CORONGIU | |
| 21 | 26 |
D |
FLUMENDOSA A GADONI |
| 22 | 29 | FLUMINEDDU A STANALI | |
| 23 | 30 | SA PICOCCA A M.TE ACUTO | |
| 24 | 31 | MOGORO A S. VITTORIA | |
| 25 | 35 | RIO LENI A VILLACIDRO | |
| 26 | 43 |
D |
ALTO FLUMENDOSA AGGREGATA |
| 27 | 50 |
D |
FLUMENDOSA A M.TE SCROCCA AGGREGATA |
I bacini del primo tipo sono stati modellati utilizzando una procedura "least squares" appositamente scritta e la cui funzione obiettivo era definita come:
![]()
Ovviamente la somma quadratica dei residui va intesa effettuata solo per quegli indici che corrispondono a valori osservati di deflusso.
Per i gruppi del secondo tipo si è tentato con successo di modellare simultaneamente tutti i bacini componenti ciascun cluster sfruttando così al massimo le informazioni contenute nei dati osservati. La funzione obiettivo era definita come somma delle funzioni obiettivo relative, questa volta, ai bacini totali componenti il cluster.
Dato il gran numero di parametri coinvolto nella modellazione dei cluster si sono utilizzate delle procedure di calcolo basate sul metodo del "simulated annealing" [9] (derivante dal metodo Monte Carlo), essendosi dimostrato in grado di garantire grande stabilità e robustezza nella stima dei parametri. Il risultato della modellazione appare incoraggiante soprattutto quando si tenga conto della scarsa qualità e della lacunosità dei dati osservativi di partenza.
Il parametro utilizzato per valutare la qualità dei fit è il rendimento h definito dall’espressione:
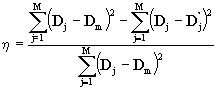
ove Dj e D'j rappresentano, rispettivamente, i deflussi osservati e calcolati relativi all’intervallo di tempo j-esimo e Dm la media dei deflussi osservati estesa agli M valori disponibili.
5.3 Modello temporale del rumore
In quei casi in cui il rendimento della funzione di trasferimento è elevato, il problema della modellazione del rumore risulta relativamente poco importante e tale considerazione giustifica la scelta di procedere separatamente alla stima dei parametri del modello principale e del modello del rumore.
Si è ritenuto di operare una standardizzazione preliminare mese a mese del rumore Ri,k nell’ipotesi che ciò fosse sufficiente ad assicurare la stazionarietà della serie trasformata e, conseguentemente, si è stabilito di interpretare quest’ultima mediante un semplice modello autoregressivo del primo ordine, trascurando anche l’eventuale presenza di fenomeni di persistenza e periodicità.
Posto, quindi, per la serie standardizzata:
R*t = (Ri,k - mk{R})/sk{R}
ove mk{R} e sk{R} sono rispettivamente le medie e gli scarti delle singole serie mensili del rumore e t è l’indice temporale espresso come:
t = 12 (i-1) + k
si è adottato, in definitiva, il modello:
R*t = F R*t-1 + at
avendo indicato con at il residuo che, per ipotesi, deve intendersi serialmente autoscorrelato e indipendente da R*t-1. La stima del parametro autoregressivo F in base al classico criterio di minimizzazione della varianza del residuo è immediata poiché essa risulta identicamente pari al coefficiente di autocorrelazione seriale di passo unitario relativo alle serie globali standardizzate. Le serie del residuo ottenute sono, ovviamente, a media nulla, entro i limiti consentiti dagli arrotondamenti.